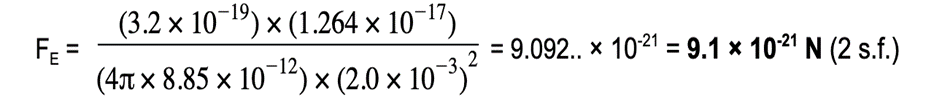2023 ELECTRICITY AND MAGNETISM

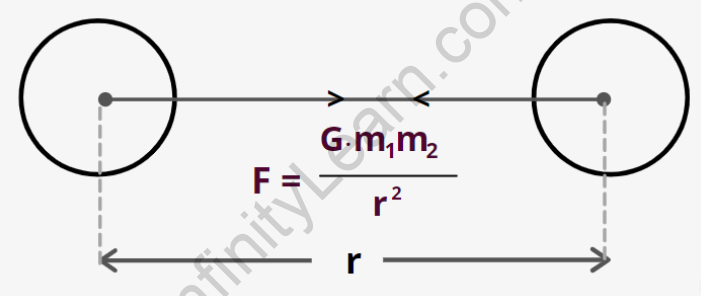
Coulomb’s law forces between two point charges

Natural gravitational force and electric force are concepts. The strengths can be easily compared by determining the ratio of forces in different cases.Coulomb’s law states that the force of attraction or repulsion between two charged things is directly proportional to the product of their charges and inversely proportional to the square of their distance.
It has an effect on the line that connects the two charges which are called point charges.

Universal Gravitational law of gravity states that:

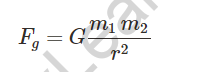
Where m₁ and m₂ are the masses of two bodies separated by r.

The gravitational constant is symbolised by the letter G. 

Electrostatic force

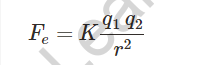
Gravitational Force – According to the universal law of gravitation, every object in the universe attracts another object with a force equal to its mass.

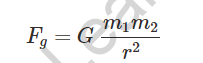
It obeys the inverse square law, which states that gravitational force is always attractive in nature.

Coulomb’s law states that two charged particles with charges q1 and q2 separated by a distance r exert an electrostatic force on each other given by

k has the value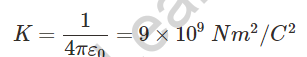 

It can be either attractive or repulsive in nature; for similar charges, it is repulsive; for opposite charges, it is attractive.

Coulomb’s law states that “the force of interaction between two point charges is directly proportional to the product of their magnitudes and inversely proportional to the square of their separation distance.”

Limitations of Coulomb’s Law

• The law only applies to point charges at rest.
• Coulomb’s Law can only be applied when the inverse square law is followed.
• When charges have an arbitrary shape, it is difficult to apply Coulomb’s law because we cannot determine the distance’ between the charges.
• The law cannot be directly applied to calculating the charge on the big planets.

FAQs

Electric Force Between Two Point Charges

Coulomb's Law

• All charged particles produce an electric field around it
• This field exerts a force on any other charged particle within range
• The electrostatic force between two charges is defined by Coulomb’s Law
• Recall that the charge of a uniform spherical conductor can be considered as a point charge at its centre
• Coulomb’s Law states that:

The electrostatic force between two point charges is proportional to the product of the charges and inversely proportional to the square of their separation

• The Coulomb equation is defined as:                       

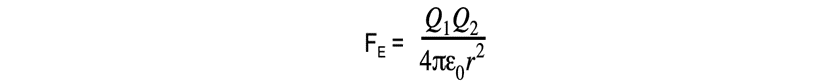
The electrostatic force between two charges is defined by Coulomb’s Law

• Where:
• F_E = electrostatic force between two charges (N)
• Q₁ and Q₂ = two point charges (C)
• ε₀ = permittivity of free space
• r = distance between the centre of the charges (m)
• The 1/r² relation is called the inverse square law
• This means that when a charge is twice as far as away from another, the electrostatic force between them reduces by (½)² = ¼
• If there is a positive and negative charge, then the electrostatic force is negative, this can be interpreted as an attractive force
• If the charges are the same, the electrostatic force is positive, this can be interpreted as a repulsive force
• Since uniformly charged spheres can be considered as point charges, Coulomb’s law can be applied to find the electrostatic force between them as long as the separation is taken from the centre of both spheres

https://www.savemyexams.co.uk/a-level/physics/cie/22/revision-notes/18-electric-fields/18-1-electric-fields/18-1-1-electric-fields--forces-on-charges

Worked Example

An alpha particle is situated 2.0 mm away from a gold nucleus in a vacuum. Assuming them to be point charges, calculate the magnitude of the electrostatic force acting on each of the charges.Atomic number of helium = 2Atomic number of gold = 79Charge of an electron = 1.60 × 10^-19 C

Step 1: Write down the known quantities

·          

• Distance, r = 2.0 mm =2.0 × 10^-3 m

The charge of one proton = +1.60 × 10^-19 C

An alpha particle (helium nucleus) has 2 protons

·          

• Charge of alpha particle, Q₁ = 2 × 1.60 × 10^-19 = +3.2 × 10^-19 C

The gold nucleus has 79 protons

·          

• Charge of gold nucleus, Q₂ = 79 × 1.60 × 10^-19 = +1.264 × 10^-17 C

Step 2: The electrostatic force between two point charges is given by Coulomb’s Law

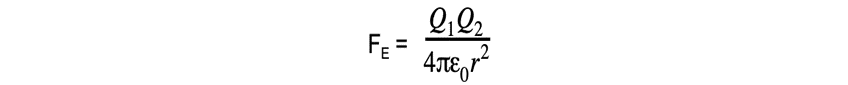
Step 3: Substitute values into Coulomb's Law;